Investment Performance Fees and Shareholder Equalization

Shortly defined, shareholder equalization is an umbrella term for all methods used to ensure fair share of performance fees for each investor (shareholder) in a fund. As mentioned in my previous related article, performance fee calculation with a general High Watermark (HWM) is quite simple and straightforward if there are no inter-period subscriptions or redemptions. But if there are inter-period cashflows, the calculation becomes more complex and some fairness concerns arise like the claw-back or free-rider syndromes that I will explain shortly. You will also see that these syndromes are actually side effects of a crude assumption, namely general HWM for all shareholders, that are tried to be corrected with some complicated adjustment methods like contingent redemption, equalization factor etc.

All these complicated adjustment methods under the name equalization will not be necessary at all if High Watermark condition is applied for each individual subscription lot of shareholders (i.e. individual HWM).

There are some other performance measurement methods based on time value of money (TWM) without any HWM condition. This article is about equalization in the context of calculation methods with HWM.

Introduction

All performance fee calculations are based on the value appreciation of the shares of a fund within a given payment period. The value appreciation can also be measured relative to a benchmark, in which case we talk about relative returns or outperformance.

In the simplest case for example, if the Net Asset Value (NAV) of a fund’s share increase from $100 to $150 within a payment period, say a quarter, the portfolio manager who is responsible for the active management of the underlying assets (i.e. timely selling or buying securities according to the predefined investment strategy of the fund, as declared in the fund prospectus) gets a certain percentage, say 5% (quarterly rate) of the value appreciation $50 as performance fee per share. If there are totally 1000 shares in the fund, the portfolio manager gets a total of $2500 (1000 x $2.5) as performance fee for the payment period.

Additional performance measurement and fairness criteria like HWM (High Watermark), hurdle rate, hard spread, benchmark returns and especially equalization make some performance fee calculations seem too complicated at first sight. But once the artificial atmosphere of complexity caused by the finance jargon used is demystified, and the mathematical meaning of the criteria used are clearly defined, one realizes that the calculation itself is not so complex at all.

In the most basic performance fee calculations one doesn’t need to keep track of the subscriptions (share purchases, also called lots) or redemptions (selling shares back to the fund) at all within the payment period; it is sufficient to know the period begin and end values of the shares.

In the more refined performance fee calculations with higher precision and fairness standards it is necessary to keep the track of individual subscriptions along with key information like subscription date, shareholder, subscription NAV, current number of shares after redemptions, and current individual HWM.

Shareholder equalization means calculating performance fees with higher precision and fairness standards through a two-step indirect logic (i.e. adjustments) which is typical for accountants and legacy systems constrained by existing practices and implementations. As in every process with adjustments, the performance fees are calculated first with some oversimplified assumptions. In the second step, some complex adjustments (i.e. equalization factors, shares etc.) are added on top of these first-step intermediate results to achieve a higher precision. In other words, the errors and deviations caused by the oversimplified assumptions (like a general HWM applied for all shares) are partially corrected by the equalization adjustments. See the reference document by Dermot Butler (March 2009), which includes a very useful overview to the general requirements on the equalization process:

1. Fees are allocated fairly and equitably among investors
2. The is a single and common NAV per share value
3. NAV per share accurately reflects the fund’s performance

Definition of terms

Payment period: Period related with performance fee payments to the portfolio manager of the fund. For example, “payment period = quarterly” means, the portfolio manager gets his performance fees, if there is any, at the end of each quarter.
Pending performance fees due to intermediate redemptions (i.e. redemption of shares before the period-end) can either be paid at once (instant crystallization in finance jargon), or accumulated (i.e. accrued) to be paid at the end of the payment period (period-end crystallization in finance jargon).

Synonyms: HWM setting frequency

NAV period: Period related with the declaration of subscription and redemption prices (i.e. NAVs per share). For example, “NAV period = weekly” means, fund shares can be purchased or redeemed weekly. Subscription NAVs (usually called gross NAV) can be different from the redemption NAVs (usually called net NAV excluding accrued performance fees) depending on the performance calculation method applied.
Synonyms: Dealing period, NAV publishing period

HWM (High Watermark): Maximum historical period-end NAV. The HWM criterion is used to prevent the portfolio manager earn performance fees solely from the fluctuations in NAV. The measure of performance is the difference between period-end NAV and HWM.
Performance fee = Fee rate x max (0, (period end NAV – HWM))
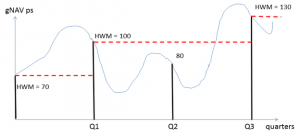
To understand HWM, consider the NAV per share development from Q2 to Q3 (quarters) in the figure below:

Dashed red lines show the general HWMs as historical maximum NAVs. “Payment period = NAV period” represents the simplest case in which there are no inter-period subscriptions and redemptions. Thus, transactions can occur only at the end or beginning of each period.

The fund performs (i.e. a value increase) in the first quarter. Assuming a performance fee rate of 5% per quarter, portfolio manager gets a performance fee of ($100 – $70) x 5% = $1.5 per share. In the next payment period (Q1 – Q2) there is no performance fee due to the drop in NAV from $100 to $80.

Third one (Q2-Q3) is the critical period to understand the significance of a general HWM. There is a value appreciation from $80 to $130, but the portfolio manager will get only 5% of the difference between 130 and 100 (current HWM) because the NAV of 100 CHF per share was already reached by the end of the first quarter.

General HWM means a global HWM which is valid for all shares in the fund independent of their individual subscription dates and NAVs. With the term general I want to distinguish between global HWMs and individual HWMs (i.e. HWM value per each subscription lot).

The theory of fair performance fees

Depicted in figure 1 was the simpler case where there are no inter-period transactions (i.e. both payment period and NAV period are defined as quarterly).

What if inter-period (payment period) transactions are possible? What if for example, payment period is quarterly again, but NAV period (i.e. dealing period) is daily? Only period-end values (i.e. NAV per share and number of shares) then won’t be enough to calculate performance fees. We will need to keep track of individual subscriptions and transactions within each payment period.

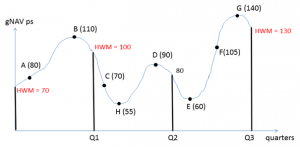
Some shareholder pays more, some less than deserved if the simple general HWM method is stubbornly applied for cases with inter-period transactions.

Consider the share purchased at time point B in the figure 2. If the performance fees are calculated with the simple HWM method that ignores the consequences of inter-period transactions, the amount of fees will be ($100 – $70) x 5% = $1.5 per share. Is this fair? No. This is $1.5 more than the portfolio manager deserves.

From the perspective of the shareholder subscribing to the share(s) at time point B there is no value appreciation from B to Q1. On the contrary, his NAV per share dropped from $110 to $100. Actually, the shareholder should have paid no performance fees at all for his shares subscribed at time point B.

In fact, all shareholders with subscriptions within the first quarter pay more performance fees than deserved due to the nature of NAV development (all subscriptions are above HWM $70). B with its maximum subscription price ($110) of the quarter is the most unfair and unfortunate case from the perspective of the shareholder.

Similarly, the shareholder who subscribed to a new share at time point G in the third quarter (Q2-Q3) pays an unfairly high amount of performance fees (($130 –$ 100) x 5% = $1.5 per share) considering that there is no value appreciation from G to Q3.
There are not only unlucky losses, but also lucky escapes from the perspective of investors, like the cases C, H and E as depicted in figure 2.

H for example, pays no performance fee at the end of the second quarter, even though the value of his shares appreciates from $55 (subscription NAV) to $80 (period-end value). E pays only for the value appreciation from $100 (HWM) to $130 at Q3, even though his shares gain in value from $60 to $130!

The subscriptions (i.e. lots) in the third quarter whose NAV are below the current HWM ($100) like E pay lower fees than deserved, and the subscriptions whose NAV are above the current HWM like F and G pay higher fees than deserved. In a sense, unlucky shareholders like F and G subsidize for the deficiency of lucky shareholders like E (claw-back syndrome).

C is another lucky case from the perspective of the shareholder. He pays no fee at the end of the second quarter (Q2) even though his shares appreciate from $70 to $100 per share. In a sense, this shareholder profits from the history of NAV development in the first quarter, in which some other shareholders already paid performance fees for the gain in value from $70 to $100 per share (free-rider syndrome).

All these unfair fee payments occur because two potentially erroneous assumptions (i.e. oversimplifications) are implicit in the simple general HWM method that ignores the effects of inter-period transactions:

1. Payment period (HWM setting frequency) > NAV period (dealing period), but there are no inter-period transactions, or
2. Payment period (HWM setting frequency) = NAV period (dealing period); shares can be redeemed only at the beginning or end of each payment period

Individual HWMs (HWM per each subscription lot) for fair performance fees

The above analysis should make it clear that we need to keep track of the transaction history in order to be able to calculate the performance fees with higher precision and fairness. The question is, what minimal information about the transaction history do we need to calculate performance fees for each payment period? Do we need to keep the whole transaction history in mind, or only a simplified summary of it?

The following analysis will show that we don’t need to store the whole history of transactions with its all details. We need only a summary, or a projection of the transaction history, namely only the list of individual HWMs for each subscription lot to calculate the performance fees for any payment period.

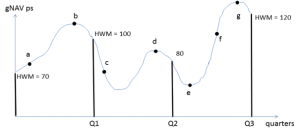
Let’s start the analysis with the share(s) purchased at time point A. The fair amount of performance fee to be paid at the end of the first quarter should be based on the value appreciation from $70 (subscription price) to $100 (period-end NAV). There should be no performance fees at the end of the second quarter (at Q2 in figure) because NAV drops from $100 to $80.

Now comes the critical question: What should be paid at the end of the third quarter? The performance fee should be equal to FeeRate x ($130 – $100) per share. Observe that $100 was the highest historical period-end NAV for A, for which a performance fee was already paid. In that sense, $100 as period-end NAV at Q1 was the individual HWM of A from Q1 to Q3. From the time point Q3 on (i.e. in the 4th quarter) $130 is the individual HWM of A.

What if the share purchased at A is redeemed at time point F with a NAV of $110? The value appreciation should again be calculated with respect to the current individual HWM of A in the third period. The performance fee due to redemption at F will be equal to FeeRate x ($110 – $100).

We can generalize this observation. Subscription NAV is the initial individual HWM of every lot, until it meets a higher period-end NAV in future. When a lot meets a higher period-end NAV as A meets at Q1, this period-end value becomes the new individual HWM value for the next period.

Bad news: We need to keep track of the individual HWM of each subscription lot to calculate performance fees.

Good news: Once we updated the list of individual HWMs per each lot at the end of a period, we can forget about other details of the transaction history. We need only the individual HWMs at the beginning of each period, as the state information of the fund, to calculate the performance fees accurately at the end of the period.

For example, in order to calculate the performance fee for A at the end of the second quarter, you only need to know that the individual HWM was $100 at the beginning of the period. You don’t need to know the previous HWM, or the subscription price of A.

Limited meaning of a general HWM in cases with inter-period transactions

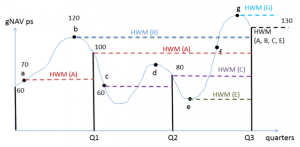
You may already have realized that a general HWM which is by definition common for all shares loses its meaning when there are inter-period transactions with different subscription and redemption NAVs compared to period-end

What does a general HWM mean at all if there are inter-period transactions? In order to check this we can ask: What conditions must be satisfied so that the general HWM is equal to the individual HWM of every subscription lot? In other words, under which circumstances is the general HWM the real global HWM of every lot?

Answer: A general HWM of a payment period is also the global individual HWM of every share only if
a) Subscription price of the share is lower than the current general HWM of the period, if the share is purchased in a previous period
b) Subscription price of the share is exactly equal to the current HWM of the period, if the share is purchased within the current period

These are but crude and unrealistic assumptions. In other words, general HWM is a kind of generalization that adds more complexity to the calculation model by creating a necessity for subsequent correction adjustments. Notwithstanding, the use of a general HWM in the first step of some performance measurement methods (to be corrected then by equalization adjustments in the second step) practiced today is actually the main source of unfairness in fee calculations.

For example, $100 is the general HWM in the second quarter in figure 4. But it is not the single global individual HWM because there are some higher subscription NAVs in the first quarter like B; the individual HWM of B is higher than 100 in the second quarter.

Complex equalization adjustments are not needed if the performance fees are calculated with individual High Watermarks. It is also easier to understand individual HWM method conceptually because it is the result of direct logic without confusing accounting-style adjustments.

I plan to write more about the mathematics of individual HWM method in a future article. It will be about:

• Reference matrix to store subscription lot data per each shareholder, and corresponding individual High Watermarks
• Fees paid or accrued at inter-period redemptions
• Individual HWM updates at each period-end
• Redistribution of shares at each period-end for a common NAV for every shareholder

Tunç Ali Kütükçüoglu, 18. April 2012

References and recommended resources

• Equalisation, is it worth the head ache? (March 2009)
• Your Guide to Performance Fees from insightinvestment.com (pdf file, search in google)

Copyright secured by Digiprove © 2012 Tunc Ali Kütükcüoglu