Following video shows the Simple Performance Fee calculation model that was introduced in a previous article in action.
In the video above I analyzed the behavior of the performance function by varying the hurdle rates from zero to 5%. In this article I want to show you another example of behavior analysis by comparing the results obtained first with, and then without relative high watermarks (rHWM condition). Related function and demonstration scripts (matlab and R) can be downloaded from the download page. In these scripts you can see the formulas that generate the hypothetical NAV per share values and benchmark returns for this example.
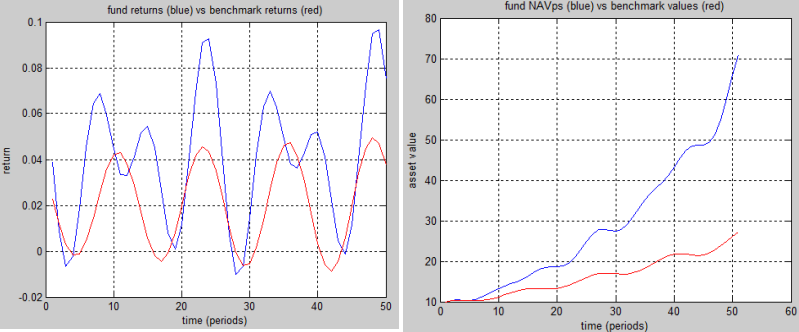
The hypothetical fund and benchmark returns for 50 periods are depicted in the graph above. Fund returns are derived from the given NAV per share values, and absolute benchmark values are derived from the given benchmark returns by setting the initial value of the benchmark to the initial value of the fund. Note that NAV per share values become larger and larger compared to benchmark values with the given returns. At the 50th period, NAV per share (about $70) is almost three times as larger than the derived benchmark value (about $27).
Other input parameters in addition to NAV values and benchmark returns are set as follows:
Fee rate = 20% Hurdle rate = 0% Fee floor = -999999999 (i.e. no effective fee floor) Fee cap = 999999999 (i.e. no effective fee cap) Relative HWM = NO for case 1 (rHWM condition is not applied) Relative HWM = YES for case 2 (rHWM condition is applied)
The calculation results, excess returns (blue curves) and performance fees per share (red curves) over 50 periods, are shown in the graphs below.
The performance fee graph above on the right side (case 2 with rHWM) shows an interesting behavior. Performance fee per share values are negative in the near vicinity of 27. and 36. of periods even though the hurdle rate is zero. How can this happen with the relative High Watermark (rHWM) condition? This happens because the outperformance (FundReturn – BenchmarkReturn) can be negative even if the relative value (NAVps – BenchmarkValue) increases compare to the previous period. In order to understand this, we need to dig a bit deeper and have a look at the calculation logic related with rHWM.
 Because hurdle rate is set to zero, FeeBeforeCF (fee per share before floor & cap) will always be zero for the periods where the rHWM condition is not satisfied. This means, negative FeeBeforeCF values are only possible for the periods where the rHWM condition is satisfied. We can than skip the first part of the equation (if rHWM is not satisfied) and focus on the second part.
Because hurdle rate is set to zero, FeeBeforeCF (fee per share before floor & cap) will always be zero for the periods where the rHWM condition is not satisfied. This means, negative FeeBeforeCF values are only possible for the periods where the rHWM condition is satisfied. We can than skip the first part of the equation (if rHWM is not satisfied) and focus on the second part.
Note that “rHWM condition is satisfied” implies that there must be a positive increase in the relative value compared to the previous period. Is it possible that rHWM condition is satisfied even though the outperformance is negative? Yes, if the values NAV per share values are higher than the (absolute) benchmark values. Consider for example the case, where NAVps = $100 (maximum value so far), fund return = %2, banchmark value = $50 and benchmark return = 3%, rWHM = 50 (100-50). In this case, the increase in relative value will be positive for the following period ((102$ – 51.5$) -50$) even though the outperformance is negative (2% – 3%).
Exactly the same case occurs in our example as the following graph illustrates. Change in relative values (blue curve) versus outperformance (red curve):
 As depicted in the graph at left, change in relative values is positive around the 36th period even though the outperformance is below zero.
As depicted in the graph at left, change in relative values is positive around the 36th period even though the outperformance is below zero.
Note that negative performance fees would not occur if the rHWM condition is applied without a benchmark, provided that hurdle rate is kept at zero. Without a benchmark, outperformance = fund performance, and relative value = NAV per share (fund value). That is, without a benchmark, outperformance cannot be negative if relative value increases.
Tunç Ali Kütükçüoglu, 13. April 2012
Matlab and R files for the demonstration of the examples explained in this article can be downloaded from the download page.
Related content
 Copyright secured by Digiprove © 2012 Tunc Ali Kütükcüoglu
Copyright secured by Digiprove © 2012 Tunc Ali Kütükcüoglu


